高校受験に必要な応用力がつく!わからない問題にあたった時の考え方

高校受験の勉強において、わからない問題に対応する力はとても重要です。
いくら勉強をがんばって苦手をなくしていっても、入試問題でわからない問題にあたることはあります。また、実際は知っている知識を使って解ける問題も、形が変わっていて気づけないこともあります。
そのときに、わからない問題に対応する力があるかないかによって合格の可能性も変わってきます。わからない問題にあたっても、対応する力があればあきらめずに点数が取れるのです。
わからない問題にあたったとき、何とか答えを出すために考えようとしても、どういう風に考えれば良いかわからなければ、考えることもできませんよね。
ここでは、わからない問題にあたったときに答えを出すための考え方を説明します。この方法は、数学や理科などの応用問題を解くときに使える方法です。
わからない問題にあたったときは「分析する」

わからない問題にあたったときは、「分析する」ことで答えに近づくことができます。分析すると言われてもピンとこない人も多いと思うので、もう少し簡単に説明してみます。
「分析する」というのは、問題をひとつひとつ整理していくつかのまとまりに分けたり、どのように問題を解いていくのかを色々な角度から調べたりすることです。
これだけ聞くと、「なんだか難しそう…」と思うかもしれませんが、決してそんなことはありません。具体的なやり方がわかり、繰り返し練習して慣れていくことでだんだんと身についていきます。
では、ここからは「分析する」方法について、具体的に説明していきます。
「分析」して答えを導き出す方法
分析の仕方には、大きく分けて次の3つがあります。この3つの方法は、数学や理科が得意な人は自然とできていることです。しかし、数学や理科が苦手な人でも、やり方さえ分かれば得意な人と同じようにできるようになります。
1.具体例を挙げてみる
2.グラフや図形を描いてみる
3.答えから逆に考える
それでは、ひとつひとつ具体的に説明していきます。
1.具体例を挙げてみる
例えば、「xを求めよ」という問題に対して「xが1ならどうなるか、2ならどうなるか、3なら……」と具体的な状況を書き出し、表にする方法です。表が書ければ、法則性が見えてきて式を作ったりすることができます。
例えば、「100円のみかんと150円のりんごを合計14個買って1600 円を支払いました。りんごは何個買ったでしょうか?」という問題があったとします。
これは一次方程式の問題ですが、一次方程式の解き方がわからなくても、みかんとりんごの数をそれぞれ(0個、14個)(1個、13個)(2個、12個)…と当てはめて計算していき、1,600円になる組み合わせを探すことで解くことができます。
このように、数字を当てはめて具体例を挙げていくことで、解き方が分からない問題でも答えにたどり着くことができます。
2.グラフや図形を描いてみる
これは図形の問題などを解くときに使える方法です。
まずは、問題の内容に沿ってできるだけ正確にグラフや図形を描きます。これだけでも、解き方が見えてくることがあります。
図が描けたらさらに、グラフや図形にわかっている長さ、求めたい部分をxとおいたときの式などを書き込みます。その時点で、表を書いたときと同じく式を立てることができるのです。
少し難しいかもしれないので、簡単な問題で見てみましょう。
例えば、半径が3cm、中心角が90°のおうぎ形の面積を求める問題の場合。
解き方がわからなくても、とりあえず図を描いてみます。

おうぎ形の図が描けたら、半径が3cmと中心角90°という情報も書き込みましょう。
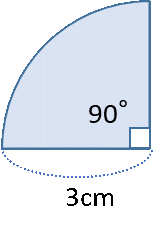
この図から、90°のおうぎ形の面積は、同じ半径の円の大きさの4分の1ということに気付く人もいると思います。そうすれば、円の面積の求め方さえわかれば、それを4で割ることで面積を出すことができます。
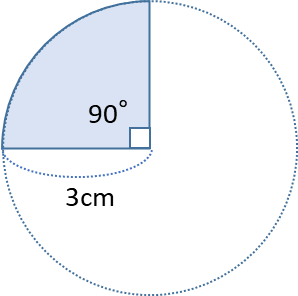
このように図を描いて考えることで、おうぎ形の面積の求め方がわからなくても解くことができます。
実際はもう少し難しい問題で使いますが、ポイントは、“図やグラフで表せる問題はとりあえず図をなるべく正確に描くこと”、そして、“分かっている情報をすべて書き込むこと”です。
3.答えから逆に考える
問題を素直に前から読んで考えていくのではなく、答えの側から考えてみることで、解答を導き出すことができる場合があります。
単純な例として、三角形の面積を求める問題を取り上げてみましょう。いきなり「どうやって面積を出そうか」と考えるのではなく、「面積を求めるためには何が必要か」と考えるのです。
そうすれば三角形の底辺や高さを求めればいいのだと気づき、その方向で考えを進めることができます。
例えば、数学の証明問題「AB = DC、AB // DCの△ABCと△CDAがあったとします。このとき、角ABC = 角CDAであることを証明しなさい。」という問題を解く場合。
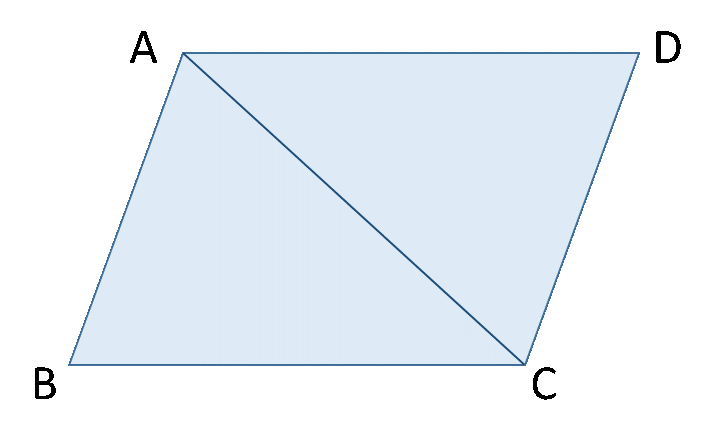
角ABC=角CDAを証明するためには何が必要かを考えると、△ABCと△CDAが合同であることが言えれば、角ABC=角CDAが証明できそうだ!と気づくと思います。
このように、答えの側から、答えを出すためには何が必要なのか?を考えることで、答えの出し方が分かる場合があります。普通に考えてみてわからない場合は、答えの方から逆に考えてみるようにしましょう。
まとめ
以上、わからない問題を解くための考え方について説明しました。
わからない問題にあたったときは、
1.具体例を挙げてみる
2.グラフや図形を描いてみる
3.答えから逆に考える
この3つの方法で考えてみるようにしましょう。
普段の勉強のときにも、わからない問題にあたったときにすぐにあきらめて答えを見るのではなく、一度自分で考えてみることが大切です。
わからなくても色々な角度から考えることで、問題を解決する力やひらめきの力がついてきます。そうすることで、高校受験の入試問題でわからない問題にあたったときも、しっかりと点数を取ることができるようになります。
今回の内容が難しいと感じる場合は、もう少し基本的な勉強方法から身につけていく必要があります。
基本的な勉強方法については、次のページで紹介していますので、最初から順番にチャレンジしてみてください。
すべての勉強を効率的にする学習の作法って?

学習の作法は、学校でいつもトップの成績を取っているような“できる生徒”が当たり前にやっている勉強法を細かいステップに分解してわかりやすく説明したものです。
この学習の作法を習得すれば、すべての勉強が効率的に進められるようになり、勉強すれば確実に結果を出すことができるようになります。


