苦手な人が多い数学の証明問題をプロが徹底解説

ここでは、高校入試の数学の問題の中でも苦手な人が多い証明問題の解き方について、細かく説明していきます。
証明問題はズバリ、得意不得意がはっきり分かれる分野だと思います。数学の他の問題と違って計算がなく、「○○は△△である」のように文字通りある事柄を「証明」していくというものです。
数学らしい計算を使わずに、言葉で『国語的』に説明をしていくので、順序だてて説明する力もそうですが、図形を見た瞬間に「この条件ならこの辺の長さが同じだ」「この角度が同じならこことここも同じだ」というように、『気づき』の力も必要となってきます。
「そういうのは苦手だから自分には無理だ…」とあきらめる人もいると思いますが、“順序だてて説明する”ことも、“気づく”ことも正しい方法で練習すれば誰でもできるようになるのです。
その『気づき』の力を高めるためには、色々な図形の性質をしっかり覚えておく必要があります。また、解答の書き方にはパターンがあります。それも含めて確認していきましょう。
今回は、高校入試で出題されやすい三角形の合同の証明と、相似の証明に焦点を当てて見ていきます。
高校入試に出やすい証明問題①三角形の合同
まずは三角形の合同の証明です。基本問題から見ていきましょう。
例題
下の図でAC=BD、AD=BCのとき△ABC≡△BADとなることを証明せよ。
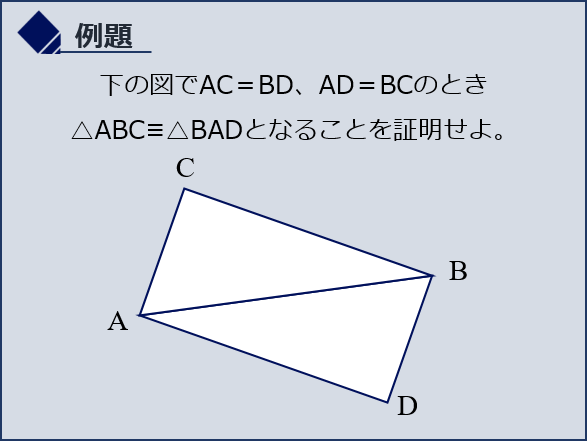
解答
△ABCと△BADにおいて
ABは共通
AC=BD (仮定)
AD=BC (仮定)
よって3組の辺がそれぞれ等しいので△ABC≡△BAD
さあ、できましたか?細かく見ていきましょう。
まず、問題を解く上で、前提として与えられた条件を仮定と良います。つまり証明問題の解答というのは、仮定から結論を導き出すことなんです。
ただ、結論は文字通り「結論」です。最終的にはこの「結論」に行き着くわけですから、最終の着地点はこの「結論」なのです。
つまり今回は
△ABC≡△BAD
が結論です。
そして問題に
AC=BD、AD=BC
とあるのでこれが仮定になります。
最後に、合同であることを証明するわけですから
三角形の合同条件
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。
に照らし合わせて考えればよい、ということです。
では実際の問題を見ていきましょう。
問
下の図でBC=DC,AC=ECのとき、AB=EDを証明しなさい。
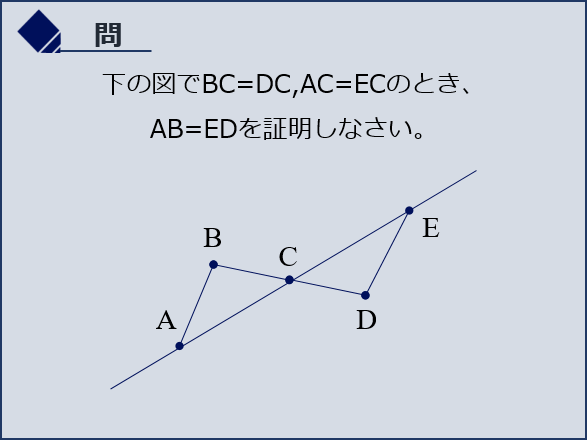
考え方
まず、問題の図を見て情報を整理します。情報を整理するとこうなります。
仮定は二つです。
BC=DC , AC=EC
そして、結論は
AB=ED
問題を解く上で、前提として与えられた条件を仮定と良います。つまり証明問題の解答というのは、仮定から結論を導き出すことなんです。ただ、結論は文字通り「結論」です。最終的にはこの「結論」に行き着くわけですから、最終の着地点はこの「結論」なのです。
そして、今回の結論はAB=EDです。しかし、この2辺が同じであることを証明するためには、この2辺が必要となる図形を合同であると証明する必要がありそうです。
今回は△ABC≡△EDCを証明すればできそうですね。(記号≡は合同という意味)そのためには∠BCA=∠DCEであるか、AB=EDであることを確かめられればよさそうです。
今回の場合は、対頂角の関係にあるので∠BCA=∠DCEであることがわかります。これらの事柄を、型にはめた形で答えていくのが証明問題を解くということです。(ちなみに三角形の基本事項は押さえておかなければなりません。
このような基本事項がわかっていないと先ほど説明した『気づき』ができないのです。 そして、証明が終了したら最後に必ず「証明が終わった」ということを報告します。たとえば「//」や「Q.E.D.」などです。
あるいは文章で「これで結論は証明された。」などと書くなど、いくつかのパターンがあります。多くの人は手間と時間がかからない「//」を用いると思います。
証明
では、証明に入っていきます。
△ABCと△EDCにおいて仮定より
BC=DC・・・①
AC=EC・・・②
また、対頂角は等しいので
∠BCA=∠DCE・・・③
①・②・③より、対応する2辺とその間の角がそれぞれ等しいので(ここがわからない人は三角形の基本条件を復習しておきましょう)
ちなみに三角形の合同条件は
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。←この条件にあてはまるわけです。
③ 1組の辺とその両端の角がそれぞれ等しい。 です。
△ABC≡△EDC
よって AB=ED (//)
このように結論に導いていきます。手順としては以下のようにすると良いでしょう。
【仮定】 問題に書いてある内容+自分で見つけた内容を整理する。
↓
合同条件により、合同な図形(今回は三角形)を見つける。
↓
【結論】合同な図形の性質により、結論に導く (//)
※図形の情報は①・②・③のようにナンバリング(番号をつける)します。
三角形の合同条件は
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。
です。
高校入試に出やすい証明問題②三角形の相似
続いて、三角形の相似の証明です。“相似“とは形は同じではあるが、大きさが違う図形のことです。
例題
下の図で△ABC∽△EBDを証明しなさい。
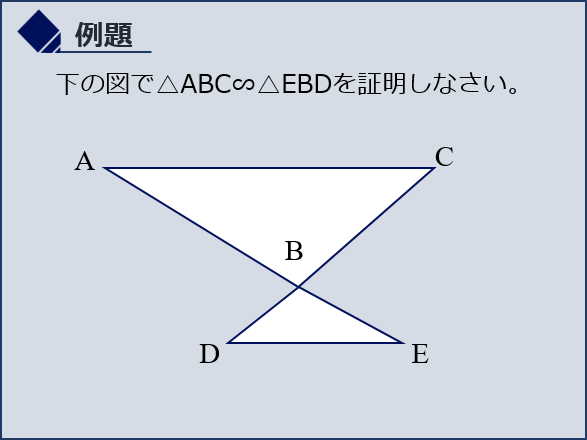
△ABCと△EBDにおいて
∠ABC=∠EBD (対頂角)
∠BAC=∠BED (AB//DEの錯角)
よって2組の角がそれぞれ等しいので△ABC∽△EBD
さあできましたか?
まず、相似な三角形の組を見つけます。コツは、この図の中にいくつの三角形を見つけることができますか?と言うことにあります。相似というのは形は同じでありながら大きさが違うというものです。図を見てください。例題は簡単ですので2つの三角形がすぐ見つかると思います。
そしてこの図からわかる情報を整理していきます。
わかるのは
①∠ABC=∠EBD が対頂角であるということ。
②∠BAC=∠BED がAB//DE(平行)の錯角であるということ。
そして最後に相似条件に照らし合わせて考えてみる。
三角形の相似条件
① 3組の辺の比がすべて等しい。
② 2組の辺の比とその間の角がそれぞれ等しい。
③ 2組の角がそれぞれ等しい。
下線部の③に該当するということです。では実際の問題を見ていきましょう。
問
下の図からDEの長さを求めよ
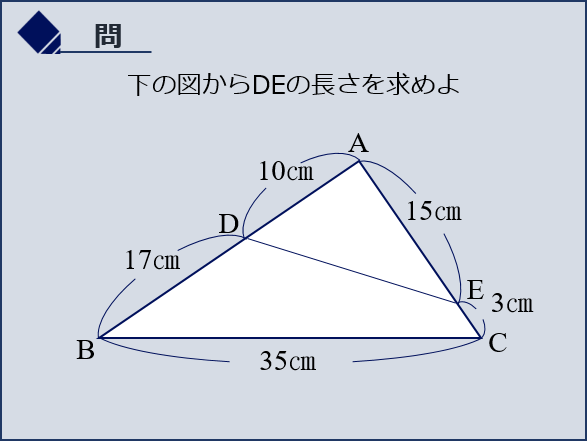
△AEDと△ABCの組が相似だと予想をするわけです。次に相似の条件がそろうか確かめます。(相似の条件は以下の通り)
向きを揃えて描きなおすとわかりやすいでしょう。
AD:AC=10:18=5:9, AE:AB=15:27=5:9, ∠DAE=∠CAB(共通)
2組の辺の比とその間の角がそれぞれ等しいという条件がそろいます。
△AED∽△ABC
ここまでで相似(相似を表す記号は∽)を証明できました。あとは、相似な図形の性質を利用して辺の長さを考えていきます。
相似図形の性質は以下の通り
① 対応する部分の長さの比はすべて等しい。
② 対応する角の大きさはそれぞれ等しい。
③ 相似な図形は対応する辺の比が等しい。←この性質に注目。
対応する辺はADとAC, DEとBCである。
もとめるDEをxとすると 5:9=x:36
9x=180
x=20
答 20cm
このように証明問題ではいくつかの「条件」や「性質」を利用して証明していくタイプの問題と、証明した結果、その図形を性質を利用して解答を出す、等レパートリーは様々です。
ですが、いずれにしてもお決まりの「型」のようなものがあります。証明問題のページらしく、『結論』から言うと、多くの問題に触れ、多くのパターンを学習することで徐々に理解も深まることでしょう。
しかし、そのためには基本事項はやはり覚えておく必要があるということです。今回の例でいけば合同条件や相似条件、またその性質など、知っておかなければそれを「利用」して問題に取り組むことができないからです。解きながら、少しずつ覚えていきましょう。
また、高校受験において重要なのが“公式”です。次の記事では高校受験指導のプロが教える、必ず覚えておきたい公式6つを紹介しています。ぜひチェックしてみてください。