【高校受験指導のプロが教える数学】必ず覚えておきたい6つの公式
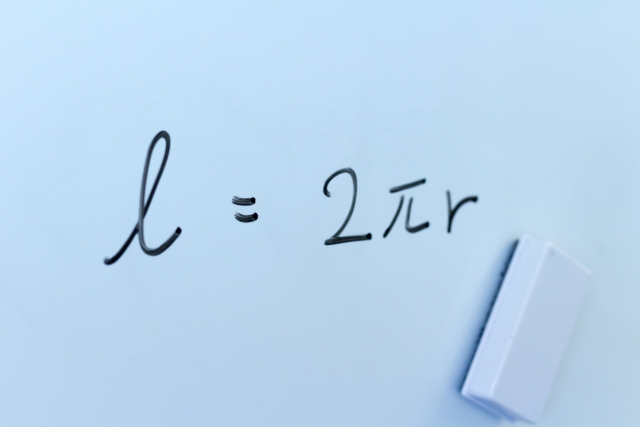
ここでは、高校受験の数学の問題によく出る公式を紹介します。
数学の問題はどれも「例題を確認し、問題を解く」→「答え合わせと復習」という流れで、時間をかけて問題演習を繰り返していかなければ解けるようにはなりません。
しかし、問題には必ず『パターン』があります。そのパターンを覚えてしまえばそんなに難しくはないのです。よく、「数学はひらめきだ」とか「数学は頭の良し悪しの左右される」「数学的センスが必要」などと言われますが、決してそうではありません。
高校受験の数学は、実は“暗記”で乗り切ることができます。暗記と言っても答えを丸暗記するのではなく、答えにたどり着くまでの『プロセス(=過程)』を暗記してしまうのです。それにはある決まったパターンがあるので、いくつか覚えることで同じような問題が解けるようになります。
では、手っ取り早くそのパターンを覚えられる裏ワザはないでしょうか。それがズバリ「公式」です。この「公式」という型にはめてしまえば後は『考える』や『ひらめきを必要とする』ことはなく、完全に流れ作業になります。ここで紹介する公式を覚えてしまって、ぜひとも「難しい」「苦手」「嫌い」な数学の問題を「流れ作業」で解いていきましょう。
1.三平方の定理
三平方の定理とは、直角三角形の3辺の長さの関係を表す等式のことを言います。
具体的には、
斜辺の二乗は直角をはさむ辺を二乗して足したものと等しい。
というものです。
たとえば斜辺をc、その他の辺をa、bとすると、c2=a2+b2
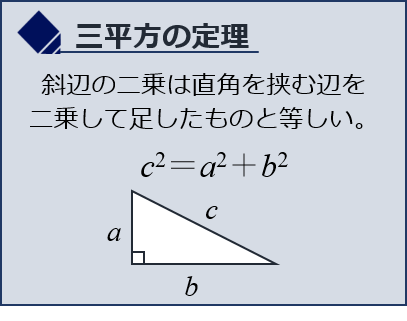
この公式はありとあらゆる場面で使用します。必ず覚えましょう。もし、「斜辺」「直角」など三角形の基本事項が理解できていない場合は、まずはその部分から復習しましょう。
2.解の公式
二次方程式の解の公式です。

二次方程式の解き方には、因数分解を使う方法や共通因数でくくる方法、平方完成を使う方法など、いろいろなパターンがあります。それらのどれを使っても解けない場合に解の公式を使います。
言ってしまえば、解の公式を使えばどんな二次方程式でも解くことができるのです。
この公式も色々な問題で幅広く使います。公式自体が難しくて覚えられないという人もいると思いますが、何度も使っているうちに体が勝手に覚えてくれます。とにかくたくさん問題を解くようにしましょう。
また、これを理解するには「平方根(ルート=√)」の分野を理解しておく必要があります。その分野の理解が足りない人は早めに復習しましょう。
3.因数分解
因数分解は公式として問題に使用するというよりは、計算問題を解くときに必要な方法です。計算問題の基本とも言えるので、確実に押さえておきましょう。
入試問題では図形問題、関数など、分野をまたいで活躍します。逆を言えば、図形、関数問題が途中まで解けていたとしても、この計算でミスをしてしまうと得点には結びつきません。頭に入れておく、というよりは徹底的に慣れておきましょう。
x²+(a+b)x+ab=(x+a)(x+b)
x²+2ax+a²=(x+a)²
x²-2ax+a²=(x-a)²
x²-a²=(x+a)(x-a)

因数分解をすばやく解けるようにするためには、ひたすら問題をこなすしかありません。
また、因数分解がよくわからないという人は、その前に習う「展開」がよくわかっていない可能性があります。因数分解の逆の作業が展開です。展開→因数分解の流れで復習し、理解を深めておきましょう。
4.円すい
円すいの表面積、側面積、体積はよく出題されますが、公式があやふやになっている人が多い部分です。この機会にしっかり覚えましょう。
まずは表面積です。
表面積……πr(L+r)

つまり、(円周率)×(半径)×(母線+半径)です。母線というのは円すいの頂点から底の円に向かって伸びている線のことです。見ての通りいたって単純な公式となっています。続いて側面積です。
側面積……πrL

つまり、(円周率)×(半径)×(母線)です。こちらもシンプルな公式となっています。表面積よりも単純です。続いて体積です。
体積…… 1/3sh
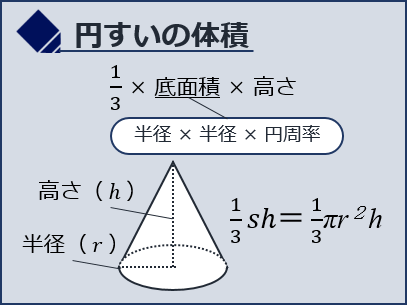
つまり、(1/3)×(底面積)×(高さ)です。ただ、底面積(=底辺部分の円の面積)はπr2
(半径)×(半径)×(円周率)なので
1/3πr2h
となります。すなわち
(1/3)×(円周率)×(半径)×(半径)×(高さ)です。
こちらは少し複雑なように見えますが、実際に計算してみるとそうでもありません。このように言葉で置き換えていくと理解しやすくなります。
5.扇形の面積
扇形の問題は、応用問題として出題されることが多いです。しっかりと公式を覚えて、いろいろなパターンの問題をたくさん解くことで、応用問題も解けるようになります。まずは公式をしっかり押さえておきましょう。
扇形の面積……πr2× x/360です。

xは中心角のことです。この形で求めるのが一般的ですが、この中心角がわかっていない状態で面積を問われることがあります。その場合は下記のように弧(扇形の外側の曲線)を使って求めます。
弧の長さで求める…… 1/2rl
.png)
つまり(1/2)×(弧の長さ)×(半径)となります。こちらの方が応用的なので、入試問題ではこの公式の方がよく使われるかもしれません。ただ、どちらも重要公式ですので必ず押さえておきましょう。
6.関数
関数には、一次関数と二次関数があります。どちらもよく出題されるので、公式はしっかり覚えておきましょう。
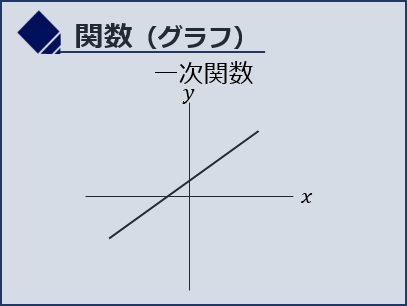
一次関数…y=ax+b 二次関数…y=ax2

一次関数と二次関数の決定的な違いは、「xが二乗になっているかどうか」です。これを次数と言います。グラフの形で見ると、下記のように一次関数が直線、二次関数が放物線を描く曲線グラフになります。

まとめ
以上、高校受験の入試問題で出題される主な公式を6つ紹介しました。
冒頭にもあったように数学の入試問題は公式を覚えたからと言って解けるというものではありません。「例題を確認し、問題を解く」→「答え合わせと復習」という風に問題演習を繰り返す必要があります。
しかし、問題のパターンに慣れ、覚えるくらいに何度も練習すればそれほど難しいものではありません。問題のパターンに慣れてくれば、入試数学に対して「応用問題が苦手…」「文系の暗記科目はできるけど…」という苦手意識もなくなることでしょう。
なぜなら、そのパターンに慣れることによって入試数学はズバリ、暗記科目になるからです。公式を「理解」し、「暗記」できるほど何度も繰り返し練習しましょう。


